The F0 algorithm was originally used in 1968 in the global food industry, and the FDA proposed it in 1976 for the pharmaceutical sterilization of Large Volume Parenteral. It is currently legally recognized in the majority of Pharmacopoeias.
It is experimentally proven that when microorganisms are immersed in saturated steam, the reaction of thermal degradation of the microorganism obeys the laws of chemical reactions.
Consider N is the number of microorganisms available in the system at the beginning, and the number reduces with the selected time t of exposure at the desired sterilization temperature can be written as:
\(\frac {dN}{dt}\)= -KN
Note: K is a constant (typical for species and conditions of the selected microorganism).
The degradation reaction (sterilization) acts as a first-order kinetic reaction where the reaction rate is proportional at every moment.
In this bimolecular reaction, the water vapor molecules take part. This the bimolecular reaction is the first order because the steam is present during the entire sterilization process, and its concentration is considered constant.
The above formula can be converted as:
\(\frac {dN}{N}\)= -K dt
By converting from base e to base 10 logarithms, the formula is:
log N = -k t + constant
k = \(\frac {K}{2.303}\)
because of changing base e logarithms to base 10.
At zero time, where t=0 and N=N0, the formula is true, i.e. log N0 = constant.
Hence,
log N = -k t + log N0
Log (N/N0) = -kt
So,
N/N0 = \(10^{-kt}\)
N0 = initial count of microorganism
t = elapsed exposure time or sterilization time
N = count of microorganism after the exposure time t
k = reaction rate constant that is depend on the species and conditions of the microorganism
The above formula reveals that the number of microorganisms reduces exponentially with sterilization time.
It can be demonstrated using the following chart where log N as the function of t.
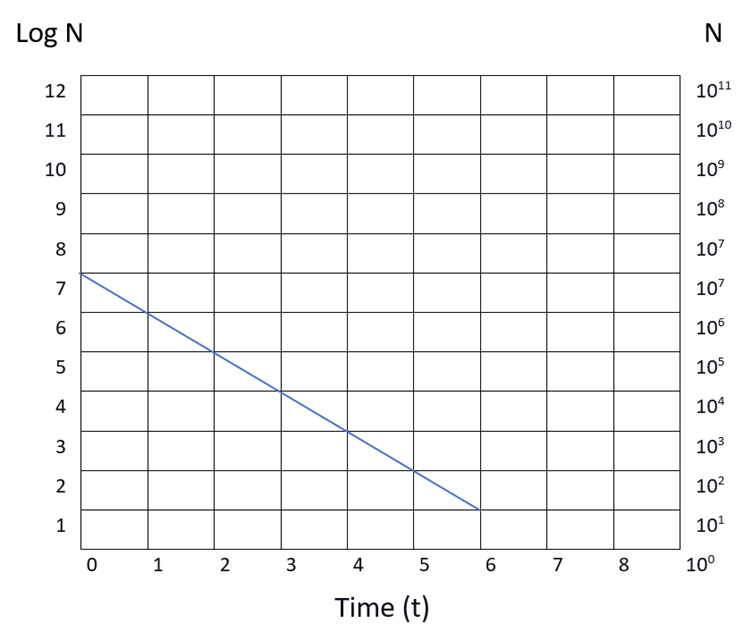
The above formula and chart indicate that the time required to reduce the microorganism population to any desired value depends on its initial concentration.
Definition of D-Value: The D-Value is defined as the decimal decay time. It means the time needed, at a specified temperature T, to decrease the microbial population by one logarithmic value (From 100% to 10%).
D-value is the time needed in minutes to destroy the 90% population of the microorganisms.
D-value can be easily calculated using the formula:
N/N0 = \(10^{-kt}\)
At temperature of 121 ℃, the D-values typically fluctuate between 0.2 and 2 minutes.
Generally, it is assumed that D121 = 1 when specific practical information is unavailable.
The result of sterilization at constant temperature can vary depending on the contaminating microbial species. D-value is on the higher side when there is mixed contamination.
As per the European Pharmacopoeia, Sterility Assurance Level (SAL) is \(10^{-6}\).
As per the United States Pharmacopoeia [USP <1229>] must requirement for sterility is Probability of Non-Sterile Unit (PNSU) = \(10^{-6}\).
For an instance, the initial microbial population is \(10^{2}\). If at 121℃ the D = 1, it requires 8 minutes to achieve residual contamination of \(10^{-6}\).
Similarly, it requires 16 minutes for the same result if D = 2, and 4 minutes if D = 0.5.
The above definition suggests when SAL is claimed as \(10^{-6}\), the probability of identifying a microbe is 1 in a million.
In summary, the effect of the D-value on microorganisms at constant temperature is tabulated below where the Initial count of Microorganisms were 100 and it was reduced to \(10^{-6}\):
| D-Value (min.) | Time Required for Microbial Reduction (min) |
| 0.5 | 4 |
| 1 | 8 |
| 2 | 16 |
D =\(\frac {t}{(log Co - log C)}\)
Where,
log in with base 10 (not base e)
t - Exposure time in minutes
Co - initial number of microorganisms
C - final number of microorganisms
Note that Sterility is a Probable Effect of Exposure time.
Suppose, the batch of the product under scope of sterilization has initial microbial contamination level is 100 (\(10^{2}\)).
When the D-value at 121 ℃ is assumed = 1, at one minute interval, microorganisms will reduce to 10 (\(10^{1}\)). After one more minute, the contamination level will reach to 1 (\(10^{0}\)). After one more minute, the microbial contamination level would be 1/10 (\(10^{-1}\)).
Theoretically, 1/10 of a microorganism is not possible; however, it can be assumed that if there are ten units (vials/ bottles), there is a likelihood of having one contaminated unit out of 10 units within the batch of sterilized units.
The z-value is the temperature coefficient of microbial destruction. z-value is the temperature that causes a 10-fold variation of D.
To better understanding of z-value, the following graph is more helpful. When the D-values are obtained from experimental data for a specific microorganism, and that is plotted on a semi-logarithmic graph as the function of the temperature T, it is observed that D-value is 1 minute at 121 ℃. D-value differs by a factor of 10 if the temperature varies by 10 ℃.
The z-values typically remain in the range between 13 and 6 for moist heat sterilization done between 100 to 130℃. The z-value is often assumed to be equal to 10 when precise data are not available.
In a practical situation, at 121 ℃, no microbe has precisely z = 10 ℃ and D = 1. But, the integrated use of these parameters in estimating F0 gives significant safety margins when dealing with microorganisms during sterilization.
F0 value is an equivalent exposure time at 121.1℃ of the actual exposure time at a variable temperature that is calculated for an ideal microorganism having a temperature coefficient of the destruction of 10 ℃.
Another definition of F0 value is "The equivalent time (minutes) at 121 ℃ or 250 ℉ given to a product during the sterilization process".
The formula for F0 Value or Equivalent Exposure Time is as follows:
F0 = Δt Σ\(10^{\frac {(T-121.1)}{z}}\)
here,
Δ t = interval of time between two successive measurements of temperature T
T = temperature of the sterilized product at time t
z = temperature coefficient (Typically assumed value is 10 ℃)
F0 = Δt Σ\(10^{\frac {(T-121.1)}{z}}\)
F0 = 30 Σ\(10^{\frac {(121.1-121.1)}{10}}\)
F0 = 30 * \(10^{0}\)
F0 = 30 * 1
F0 = 30
F0 = 30 is an ideal condition for moist heat sterilization.
At constant 110 ℃, the sterilization hold time of 30 minutes is applied; what would be the F0 value? Let's calculate.
F0 = Δt Σ\(10^{\frac {(T-121.1)}{z}}\)
F0 = 30 Σ\(10^{\frac {(110-121.1)}{10}}\)
F0 = 30 * 0.077624712
F0 = 2.32874135
F0 = 2.33
The result indicated that sterilization at 110 ℃ for 30 minutes is equivalent to 2.33 minutes of sterilization at 121.1 ℃.
F0 = Δt Σ\(10^{\frac {(T-121.1)}{z}}\)
F0 = 30 Σ\(10^{\frac {(125-121.1)}{10}}\)
F0 = 30 * 2.454708916
F0 = 73.64126747
F0 = 73.6
The result indicated that sterilization at 125 ℃ for 30 minutes is equivalent to 73.6 minutes of sterilization at 121.1 ℃.
There are chances that the sterilization cycles fail even if the sterilization hold time is completed when the average temperature observed is below 121.1 ℃.
Conversely, when the system's average temperature is above the set value of 121.1 ℃, the sterilization achieves even before the sterile hold time completes.
"It is suggested to use equivalent time (lethality) F0 when the product cannot be sterilized by steam sterilization at 121 ℃ for 15 minutes".
Reference
"A validated minimum lethality of 8 minutes expressed as equivalent time or lethality F0 with a minimum temperature of 110 ℃ is always required for sterilization by EP 10.0, 5.1.1 and the related"
"EMA Sterilization Guideline 2019"
Reference
"These "lighter" conditions are applicable only in the case the "reference cycle" of 15 minutes at 121 ℃ minimum is demonstrated not suitable for the product; they demand progressively deeper validation studies".
Reference
"Please note that an intermediate cycle with a minimum F0 of 12 minutes and a minimum temperature of 121 ℃ is called "overkill cycle" by the actual European rules".
The holding phase of a lethality-based cycle may be time-targeted as well, provided that the delivered lethality complies with the EP requirements.
Reference
I hope this online F0 value calculator was useful to you in some way. This is a fantastic post by Fedegari that discusses the F0 value and will undoubtedly broaden your knowledge.
The time (in minutes) of exposure at a given temperature which causes a one log reduction or 90% reduction in the population of a specific microorganism.
A Z-value is a number of degrees (℃ or ℉) required to change a D-value by 10-fold. In other words, it measures how susceptible a spore population is to changes in temperature.
Equivalent exposure time required for moist-heat sterilization at a specific temperature T and to a specific value of z
The equivalent exposure time for moist-heat sterilization represents the temperature of 121.1 ℃, and the Z-value (Temperature Coefficient) is considered as 10.
Number of viable microorganisms available in a unit before sterilization.
It is a number that expresses the probability of finding one non-sterile unit in a specific number of sterilized units (lot)